主要收集一些在平时遇到的但是还未形成体系的内容。

1 java相关

Class类中的getCanonicalName(), getName(), getSimpleName()

getCanonicalName() 是获取所传类从java语言规范定义的格式输出。 //getCanonicalName()=com.pinzhi.test.dao.DaoEntity
getName() 是返回实体类型名称 //getName()=com.pinzhi.test.dao.DaoEntity
getSimpleName() 返回从源代码中返回实例的名称。//getSimpleName()=DaoEntity

2 linux相关

问题1 ：虚拟机环境下Ubuntu登录后只显示桌面背景

解决方案：按alt+ctrl+F1进入命令行模式，使用sudo apt-get install ubuntu-desktop重新安装桌面

3 Python相关

yield与yield from 关键字的性质

为了探究两个关键字的性质，使用print的方式测试了他们的一些性质。代码如下：

#yield_from.py
#定义两个函数，htest()&itest()
#在主方法中调用itest()，itest()通过yield from调用htest()
def htest():
    print('htest run...')
    i = 0
    key = 0
    while i < 4:    
        n = yield key     
        if n == 4:
            p = 100    
        else:
            p = n
        key = p
        print('h[',i,']:',key)
        i += 1

def itest():
    print('itest() start')
    h = htest()
    k = 0
    h.send(None)
    while True:    
        d = yield k
        print('d=',d)
        print('yield from htest()')
        val1 = yield from htest()
        print('itest1:', val1)
        val2 = yield from htest()
        print('itest2:', val2)
        e = yield k
        print('e=',e)
        try:
            print('th:',h.send(e))
        except StopIteration as e:
            print('h error!!!')
    print('itest() end')

if __name__ == '__main__':
    t = itest()
    t.send(None)
    j = 0
    while j < 12:
        j += 1
        try:
            t.send(j)
        except StopIteration as e:
            print('error!!!')

运行结果如下:
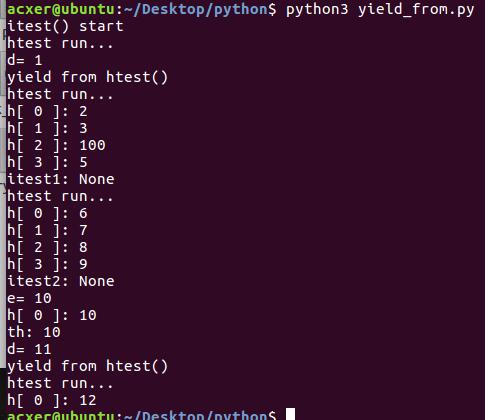
test_yield_from
由代码可以看出两个关键字有如下特点：

对于一个coroutine函数，首先要用send()方法传入一个None，开启这个函数
coroutine函数传入参数的个数，由函数内的循环次数决定（即如果为无限循环时，可能会导致另一个coroutine函数无法接收参数），传入的参数个数超过循环次数则会抛出’StopIteration‘异常
coroutine函数内通过 a = yield b或 a = yield from b（）的方式接受传入的值，若是用变量接收，变量可为任意变量，但一定要是已定义的变量，接收变量后，可通过 b = xxx或return xxx设定外部函数的返回值;若是使用yield from的方式，则要求后面的函数是coroutine函数。
参数传入是按顺序传入的。可以将yield from看做是一个数组，比如先用yield传值，后面接上一个yield from，则先将一个值传给yield，再将后面长度为yield from数组的数传入该函数中
使用yield from 方法时，若是直接传输给一个函数即yield from xxx(),每次传输都会重新开始循环；
若是使用在循环外h =coroutine() h.send(None)开启coroutine函数，在循环中用yield h接受传入的值，则每次运行都会从继续上一次的状态开始

python中的文件操作

有以下语句：

1 2	with open(filepath,'xt') as f: f.write('Hello\n')

理解为：x模式是Python3中对open()函数的拓展，用来代替W模式对一个不存在文件系统的文件操作。xt 模式下，若是filepath中的文件已存在，会抛出FileExistsError。

翻转list

有以下语句：

1 2	x = [1,2,3,4,5,6] x_trans = [x[::-1] for val in x]

理解为：对于一个list，使用索引取值时，可以加入第三个参数，即取值的步长（默认为1），值为-1表示逆序取值

np.newaxis

功能：np.newaxis是用来给数组a增加维度的
格式：a[np.newaxis和:的组合]，如a[:,np.newaxis]，a[np.newaxis, np.newaxis, :]
详解：np.newaxis在[]中第几位，a.shape的第几维就变成1，a的原来的维度依次往后排。

# 示例
a.shape=(a ,b, c)

a[:, np.newaxis].shape= (a, 1, b, c)
a[:, np.newaxis, np.newaxis].shape= (a, 1, 1, b, c)
a[np.newaxis, :].shape= (1, a, b, c)
a[np.newaxis, np.newaxis, :].shape= (1, 1, a, b, c)
a[np.newaxis, :, np.newaxis].shape= (1, a, 1, b, c)
a[np.newaxis, :, np.newaxis, :].shape= (1, a, 1, b, c)

4 机器学习相关

[《time-series-of-price-anomaly-detection》](https://towardsdatascience.com/time-series-of-price-anomaly-detection-13586cd5ff46) >一篇关于异常检测的好文章，使用python实现了不同方法在异常检测上的应用

相关算法:
孤立森林算法,过程大概为，对不同维度随机划分区间（直至区间内只剩一个点)构造多棵树，根据目标点在多棵树中的平均高度判断是否异常点
oneClassSvm，求出包裹样本的最小超球面，不在球面内的样本都认为不是想要的类

基本概念

**输入空间/输出空间: **监督学习中，属入和输出所有可能的取值集合称为输入空间和输出空间。通常输出空间远小于输入空间
特征空间：每一条样本被成作是一个实例，通常由特征向量表示，所有特征向量存在的空间称为特征空间。特征空间有时候与输入空间相同，有时候不同（例如word embbeding），不同的情况是输入空间通过某种映射生成了特征空间。

k-means:k-均值

算法实现过程

step1. 随机选取k个对象作为初始的k个簇的质心；
step2. 剩余对象使用距离公式（默认为欧式距离）分别对质心求得距离，分配点到距离最近的簇
step3. 求得各簇的均值，作为新的质心
step4.重复step2,3，直到目标函数最小化为止

k-meoids:k-中心点

算法实现过程

step1. 随机选取k个对象作为初始的k个簇的质心；
step2. 剩余对象使用距离公式分别对质心求得距离，分配点到距离最近的簇
step3. 随机选取某一簇的非中心点作为新的质心，重复step2，计算每个点与新质心和旧质心的距离变化（正/负/零）并求出总变化S，若S<0,则使用新质心
step4.重复step3，直到目标函数最小化为止

GMM，高斯混合模型（EM方法）

高斯混合模型（GMM）,是将一个事物分解为若干基于高斯概率密度函数形成的模型。其基本公式如下：
$$
P(y|\theta) =\sum_{k=1}^{K}{\alpha_{k}\phi(y|\theta_{k})}\
其中，\alpha_{k}是系数，\alpha_{k}\ge0,\sum_{k=1}^{K}{\alpha_{k}}=1;\phi(y|\theta_{k})是高斯分布密度，\theta_{k}=(\mu_{k},\sigma_{k}^{2}),\
\phi(y|\theta_{k})=\frac{1}{\sqrt{2\pi}\sigma_{k}}e^{-\frac{(x-\mu_{k})^{2}}{2\sigma_{k}^{2}}}
$$

算法实现过程

step1. 给定高斯概率公式，假设数据由k组高斯分布数据混合而成
step2. 随机指定两组高斯分布的参数（均值，方差）
step3. 使用两条概率公式对所有数据点进行划分
step4.分别求得划分结果的均值和方差，作为新一轮EM的初始参数
step5.重复步骤2-4，直到参数不再变化

参考文献：
[1]混合高斯模型（GMM）推导及实现
[2]EM算法

ID3

ID3算法是决策树方法中最具代表性的算法,以信息熵作为目标评价函数。其基础理论为信息熵理论，相关的公式如下所示：

$$
\begin{align}
&信息量：&i(y)&=- \log_{2}{P(y)} \tag{1}\
&信息熵：&H(Y)& = -\sum_{i=1}^{n}{P(y_{i})}\log_{2}{P(y_{i})}\tag{2}\
&条件熵：&H(Y|X)&=\sum_{x\in{X}}{P(X)H(Y|X=x)} \tag{3}\
&&&=-\sum_{x\in X}{P(X)}\sum_{y \in Y}{P(y|x)\log_{2} P(y|x)}\
&&&=- \sum_{x \in X}\sum_{y \in Y}{P(y|x) \log_{2}{p(y|x)}}\
&信息增益:&Grain(Y,X)&=H(Y) - H(Y|X) \tag{4}
\end{align}
$$

公式（1）为信息量的计算公式，其中，P(Y)是事件发生的概率。公式表示了一件事发生的概率越小，它所蕴含的信息量越大。
公式（2）为信息熵的计算公式，表达了Y事件发生的不确定度，就是所有可能发生的事件的信息量的期望。
公式（3）为条件熵的计算公式，表示在给X给定的条件下，Y的条件概率分布的熵对X的数学期望。
公式（4）为信息增益公式。当我们用另一个变量X对原变量Y分类后，原变量Y的不确定性就会减小了(即熵值减小)。而熵就是不确定性，不确定程度减少了多少其实就是信息增益。

算法实现过程（树构建）

step1. 分别求得各个特征与目标结果的条件熵，信息增益最大的列为最优特征列；
step2. 以最优特征列为根节点，列的值作为划分依据，对数据集进行划分，在各分支取得数据子集（值等于分支的值，并去掉该最优特征列）；
step3. 分别以数据子集为基础，重复step1,2。直到特征列为1或分支下目标类别概率为1；

参考文献：
[1]决策树之系列一ID3原理与代码实现)

C4.5

C4.5算法也是决策树算法的一种，是ID3算法的一种改进算法。算法中，与ID3的最大区别在于C4.5提出了一个新的特征选择标准：
$$
\begin{align}
信息增益率：IGR &= \frac{Gain(Y,X)}{H(X)}\
&=\frac{H(Y)-H(Y|X)}{H(X)}
\end{align}
$$
算法步骤同ID3算法过程。

参考文献：
[1]数据挖掘领域十大经典算法之—C4.5算法（超详细附代码）

感知机

感知机原理+代码可在查考文献中查看。

算法实现过程

$$
\begin{align}
&step1. w,b参数初始化，即随机选取w_{0},b_{0}\
&step2. 在数据集中选取数据(x_{i},y_{i}),若 y_{i}(w \cdot x_{i} + b) \le 0 ,说明 (x_{i},y_{i})是误分类点，需要对对应的w,b的值进行修正:\
& ;;;; w \gets w + \eta y_{i} x_{i}\
& ;;;; b \gets b + \eta y_{i}\
&step3. 计算 (y_{i}(w \cdot x_{i} + b)的值，若还是小于等于0，则重新更新w,b的值\
&step4. 重复step2,3，直到训练完所有点；\
&step5. 重复step2,3,4完成一次迭代，直到训练集中没有误分类点，得到超分界面方程\
\end{align}
$$

参考文献：
[1]机器学习——15分钟透彻理解感知机

## Fisher线性分类器判别分析问题，即：根据历史上划分类别的有关资料和某种最优准则，确定一种判别方法，判定一个新的样本归属哪一类。Fisher线性分类器是一种线性判别函数。

算法计算步骤

$$
\begin{align}
&0)有数据集合X=(x_{0},x_{1},…,x_{i}),可分为w^{0},w^{1}两组\
&w^{0}=
\begin{bmatrix}
x_{11}^{0} & x_{12}^{0} & \cdots & x_{1d}^{0} \
x_{21}^{0} & x_{22}^{0} & \cdots & x_{2d}^{0} \
\vdots &\vdots & \ddots & \vdots \
x_{s1}^{0} & x_{s2}^{0} & \cdots & x_{sd}^{0} \
\end{bmatrix},
w^{1}=
\begin{bmatrix}
x_{11}^{1} & x_{12}^{1} & \cdots & x_{1d}^{1} \
x_{21}^{1} & x_{22}^{1} & \cdots & x_{2d}^{1} \
\vdots &\vdots & \ddots & \vdots \
x_{t1}^{1} & x_{t2}^{1} & \cdots & x_{td}^{1} \
&\end{bmatrix}\ \
&1)计算每个矩阵每一列的均值：m_{1}=(\bar{x}{1}^{0},\bar{x}{2}^{0},\cdots,\bar{x}{d}^{0}),m{2}=(\bar{x}{1}^{1},\bar{x}{2}^{1},\cdots,\bar{x}{d}^{1})\ \
&2)求出新矩阵AB及两组的类内差矩阵(离散度矩阵)S{1},S_{2}:\
&A=
\begin{bmatrix}
x_{11}^{0}-\bar{x}{1}^{0} & x{12}^{0}-\bar{x}{2}^{0} & \cdots & x{1d}^{0}-\bar{x}{d}^{0} \
x{21}^{0}-\bar{x}{1}^{0} & x{22}^{0}-\bar{x}{2}^{0} & \cdots & x{2d}^{0}-\bar{x}{d}^{0} \
\vdots &\vdots & \ddots & \vdots \
x{s1}^{0}-\bar{x}{1}^{0} & x{s2}^{0}-\bar{x}{2}^{0} & \cdots & x{sd}^{0}-\bar{x}{d}^{0} \
\end{bmatrix},
B=\begin{bmatrix}
x{11}^{1}-\bar{x}{1}^{1} & x{12}^{1}-\bar{x}{2}^{1} & \cdots & x{1d}^{1}-\bar{x}{d}^{1} \
x{21}^{1}-\bar{x}{1}^{1} & x{22}^{1}-\bar{x}{2}^{1} & \cdots & x{2d}^{1}-\bar{x}{d}^{1} \
\vdots &\vdots & \ddots & \vdots \
x{t1}^{1}-\bar{x}{1}^{1} & x{t2}^{0}-\bar{x}{2}^{1} & \cdots & x{td}^{1}-\bar{x}{d}^{1} \
\end{bmatrix}\
&\quad S{1} = A’A,\quad S_{2} = B’B,\quad S=S_{1}+S_{2}\ \
&3)根据极值点推导，最优判别函数c_{1},c_{2},\cdots,c_{d}为下述方程的解：\
&S
\begin{pmatrix}c_{1}\c_{2}\\vdots\c_{d}\end{pmatrix}=
\begin{pmatrix}m_{11}-m_{21}\m_{12}-m_{22}\\vdots\m_{1d}-m_{2d}\end{pmatrix}=
\begin{pmatrix}\bar{x}{1}^{0}-\bar{x}{1}^{1}\\bar{x}{2}^{0}-\bar{x}{2}^{1}\\vdots\\bar{x}{d}^{0}-\bar{x}{d}^{1}\end{pmatrix},即
\begin{pmatrix}c_{1}\c_{2}\\vdots\c_{d}\end{pmatrix}=S^{-1}\begin{pmatrix}\bar{x}{1}^{0}-\bar{x}{1}^{1}\\bar{x}{2}^{0}-\bar{x}{2}^{1}\\vdots\\bar{x}{d}^{0}-\bar{x}{d}^{1}\end{pmatrix}\
&\quad\quad可得判别函数：y=c_{1}x_{1}+c_{2}x_{2}+\cdots+c_{d}x_{d}\ \
&4)算出A,B两组的代表判别值及临界判别值：\
&\quad \bar{y}{A} = c{1}\bar{x}{1}^{0}+c{2}\bar{x}{2}^{0}+\cdots+c{d}\bar{x}{d}^{0},\quad
\bar{y}{B} = c_{1}\bar{x}{1}^{1}+c{2}\bar{x}{2}^{1}+\cdots+c{d}\bar{x}{d}^{1},\quad \
&\quad y{0}=\frac{s\bar{y}{A}+t\bar{y}{B}}{s+t}\ \
&5)对新数据做预测判别:\
&\quad 假设有一组新数据(x_{01},x_{02},\cdots,x_{0d}),则有判别值y=c_{1}x_{01}+c_{2}x_{02}+\cdots+c_{d}x_{0d}\
&\quad\quad a)当\bar{y}{A}>y{0}时，若y>y_{0},则判别该对象属于组A,若y<y_{0},则判别该对象属于组B;\
&\quad\quad b)当\bar{y}{B}>y{0}时，若y>y_{0},则判别该对象属于组B,若y<y_{0},则判别该对象属于组A;
\end{align}
$$

拉格朗日乘子法

拉格朗日乘子法主要解决的问题是：在约束条件下取得目标函数的最优解（最值）问题。

参考文献：
[1]深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

似然比率方法

CUSUM方法

CUSUM方法的理论基础是序贯分析原理中的序贯概率比检验，这是一种基本的序贯检验法。采用了类似滑动窗口的方式，对变化点进行检测。
其基本思路为：使用一个计数器统计前后数据之间的变化，当数据的均值、方差等发生变化时，统计量会不断累计，为异常事件的发生设定一个阈值，若超过阈值则认定序列的状态发生变化。

参考文献：
[1]CUSUM算法
[2]CUSUM算法在变点检测中的应用

激活函数

$$
sigmoid: \sigma(x) = \frac{1}{1+e^{-x}}\
$$

5 tensorflow相关

API

理解tf.squeeze

squeeze(input, axis=None, name=None, squeeze_dims=None)
该函数返回一个张量，用来三处维度为1 点维度
如：tf.squeeze(inputs,[2,4]) # 删掉2维和4维

global_step

主要在滑动平均，学习率变化等场景下使用

tf.summary

够保存训练过程以及参数分布图并在tensorboard显示

tf.summary.scalar

# 用来显示标量信息，其格式为：
tf.summary.scalar(tags, values, collections=None, name=None)

#例如：tf.summary.scalar('mean', mean)
#一般在画loss,accuary时会用到这个函数。
#########
tf.summary.histogram

#用来显示直方图信息，其格式为：
tf.summary.histogram(tags, values, collections=None, name=None) 
#例如： tf.summary.histogram('histogram', var)
#一般用来显示训练过程中变量的分布情况
#########
tf.summary.distribution
#分布图，一般用于显示weights分布
#########
tf.summary.text
#可以将文本类型的数据转换为tensor写入summary中：
#例如：
text = """/a/b/c\\_d/f\\_g\\_h\\_2017""" summary_op0 = tf.summary.text('text', tf.convert_to_tensor(text))
#########
tf.summary.image
# 输出带图像的probuf，汇总数据的图像的的形式如下： 
#' tag /image/0', ' tag /image/1'...，如：input/image/0等。
#格式：
tf.summary.image(tag, tensor, max_images=3, collections=None, name=Non
#########
tf.summary.audio
# 展示训练过程中记录的音频 
#########
tf.summary.merge_all
# merge_all 可以将所有summary全部保存到磁盘，以便tensorboard显示。如果没有特殊要求，一般用这一句就可一显示训练时的各种信息了。
#格式：tf.summaries.merge_all(key='summaries')
#########
tf.summary.FileWriter

#指定一个文件用来保存图。
#格式：tf.summary.FileWritter(path,sess.graph)
#可以调用其add_summary（）方法将训练过程数据保存在filewriter指定的文件中

6 面试准备推荐阅读目录

7 框架学习

Mybatis-plus

增删改查

1
2

#To be continue…

1 java相关

Class类中的getCanonicalName(), getName(), getSimpleName()

2 linux相关

问题1 ：虚拟机环境下Ubuntu登录后只显示桌面背景

3 Python相关

yield与yield from 关键字的性质

python中的文件操作

翻转list

np.newaxis

4 机器学习相关

基本概念

k-means:k-均值

算法实现过程

k-meoids:k-中心点

算法实现过程

GMM，高斯混合模型（EM方法）

算法实现过程

ID3

算法实现过程（树构建）

C4.5

感知机

算法实现过程

算法计算步骤

拉格朗日乘子法

似然比率方法

CUSUM方法

激活函数

5 tensorflow相关

API

理解tf.squeeze

global_step

tf.summary

6 面试准备推荐阅读目录

数据结构

进程与线程

数据库

7 框架学习

Mybatis-plus

增删改查